- MemReduce 與 MemFold
- Multi-dimensional Banking
請注意有許多 Spatial 應用能夠在此找到.
Overview
General Matrix Multiply (GEMM) 是個在線性代數, 機械學習, 統計與其他領域中常見的運算. 它提供了一個相較先前教學更為有趣的權衡空間, 因為有著許多分割計算的方式. 這些包含著使用 blocking(分割為區塊), inner products(內積), outer products(外積) 以及 systolic array 等技巧. 在此教學中, 將展示如何建立使用外積分塊的 GEMM 應用, 並且留給使用者自行嘗試建立使用內積的 GEMM 版本. 後續的教學將會展示如何在其他應用中使用 shift registers 以及 systolic array, 但相同的技巧也能一併追加應用在 GEMM.
下圖的動畫顯示基本使用外積的方式計算
C = A x B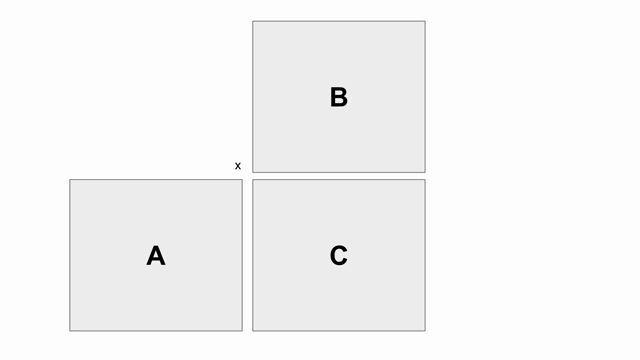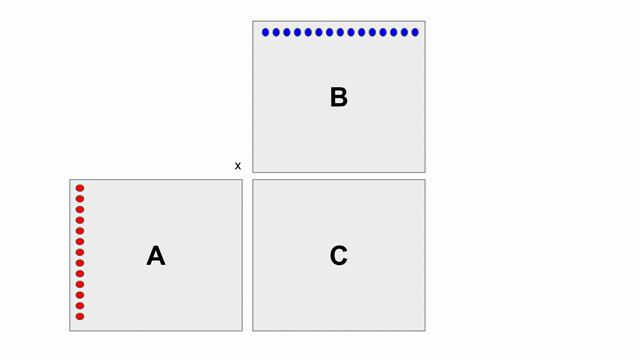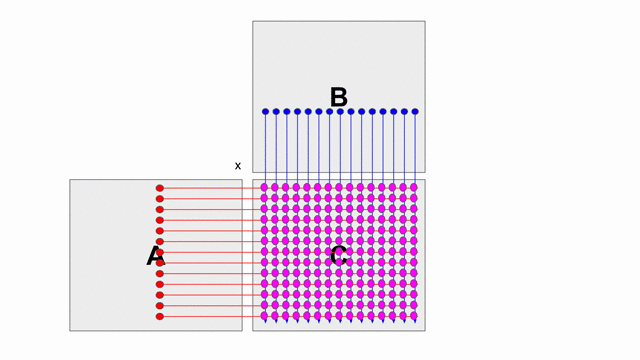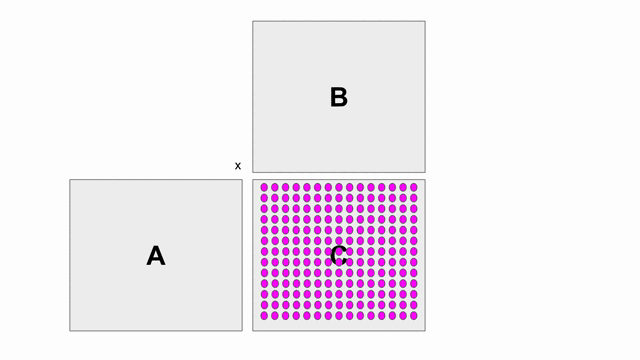
Basic implementation
import spatial.dsl._
@spatial object MatMult_outer extends SpatialApp {
type X = FixPt[TRUE,_16,_16]
def main(args: Array[String]): Unit = {
// Get sizes for matrices from command line
val m = args(0).to[Int]
val n = args(1).to[Int]
val p = args(2).to[Int]
// Generate data for input matrices A and B, and initialize C
val a = (0::m, 0::p){(i,j) => ((i + j * p) % 8).to[X] }
val b = (0::p, 0::n){(i,j) => ((i + j * n) % 8).to[X] }
val c_init = (0::m, 0::n){(_,_) => 0.to[X] }
// Communicate dimensions to FPGA with ArgIns
val M = ArgIn[Int]
val N = ArgIn[Int]
val P = ArgIn[Int]
setArg(M,m)
setArg(N,n)
setArg(P,p)
// Create pointers to matrices
val A = DRAM[X](M, P)
val B = DRAM[X](P, N)
val C = DRAM[X](M, N)
// Set up parallelizations
val op = 1
val mp = 1
val ip = 1
val bm = 16
val bn = 64
val bp = 64
setMem(A, a)
setMem(B, b)
setMem(C, c_init)
Accel {
// Tile by output regions in C
Foreach(M by bm par op, N by bn par op) { (i,j) =>
val tileC = SRAM[X](bm, bn)
// Prefetch C tile
tileC load C(i::i+bm, j::j+bn par ip)
// Accumulate on top of C tile over all tiles in P dimension
MemFold(tileC)(P by bp) { k =>
val tileA = SRAM[X](bm, bp)
val tileB = SRAM[X](bp, bn)
val accum = SRAM[X](bm, bn)
// Load A and B tiles
Parallel {
tileA load A(i::i+bm, k::k+bp)
tileB load B(k::k+bp, j::j+bn)
}
// Perform matrix multiply on tile
MemReduce(accum)(bp by 1 par mp){ kk =>
val tileC_partial = SRAM[X](bm,bn)
Foreach(bm by 1, bn by 1 par ip){ (ii,jj) =>
tileC_partial(ii,jj) = tileA(ii,kk) * tileB(kk,jj)
}
tileC_partial
}{_+_}
}{_+_}
// Store C tile to DRAM
C(i::i+bm, j::j+bn par ip) store tileC
}
}
// Fetch result on host
val result = getMatrix(C)
// Compute correct answer
val gold = (0::m, 0::n){(i,j) =>
Array.tabulate(p){k => a(i,k) * b(k,j)}.reduce{_+_}
}
// Show results
println(r"expected cksum: ${gold.map(a => a).reduce{_+_}}")
println(r"result cksum: ${result.map(a => a).reduce{_+_}}")
printMatrix(gold, "Gold: ")
printMatrix(result, "Result: ")
assert(gold == result)
}
}
上面的程式展示了如何使用內積與 tiling 來計算矩陣乘法. 在此將帶過在此程式中導入的新結構. 下圖動畫展示了在此範例中所使用的 tiling 設計.
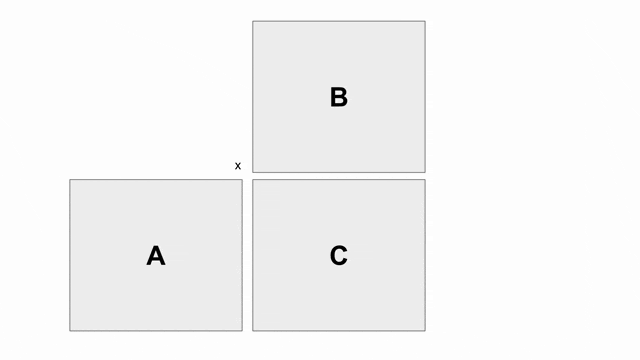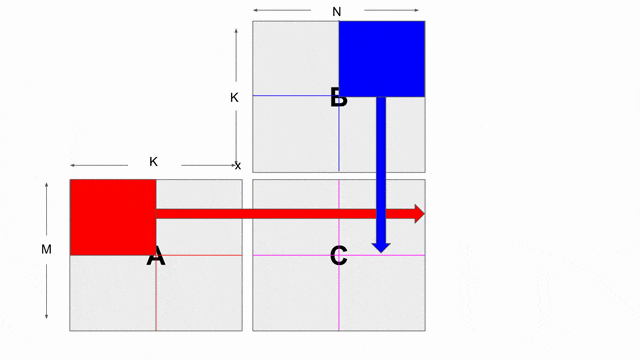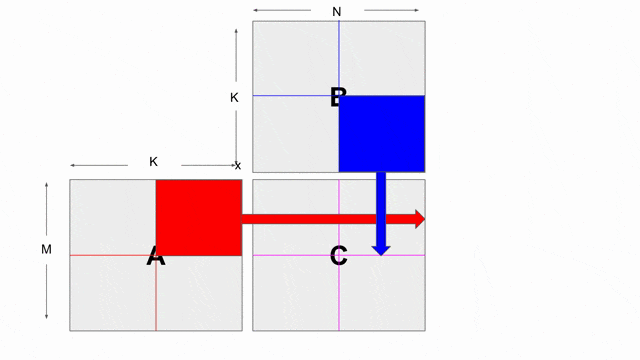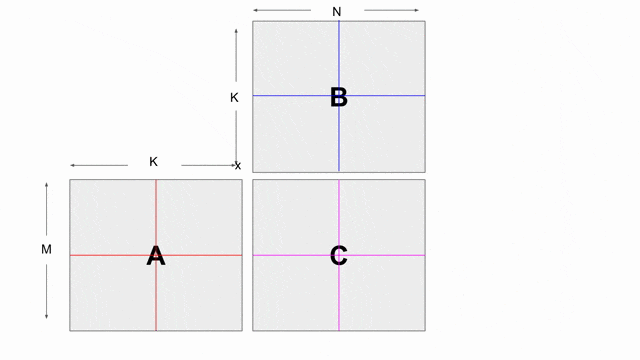
為了產生
a, b, 與 c_init 等在 Host 端的資料結構, 使用了用以產生一個 Matrix的語法. 精確地說是 (0::m, 0::p){(i,j) => … }. 這能用以產生高達 5D 的資料結構. 為了產生 c_init, 以底線來標示 iterators, 這是由於他們並沒有明確地被使用在此函數, 這在 Scala 中這是相當普遍的作法.
接著, 設定所有的平行因子為 1. 在下節中, 將進一步討論與解釋這些對於所產生硬體的影響.
在此版本的矩陣乘法中, 選擇在最外部的 loop 中透過水平掃過記憶體的方式, 一一計算不同 C 的不同區塊. 也有著其他的次序產生有效的矩陣乘法, 但此這是最小 DRAM 傳遞的方式之一.
由於這是一個一般的矩陣乘法, 並沒有保證實際上矩陣
C 有被初始化為0. 因此正確的作法是在既有存在於 C 中的數值之上做疊加. 在此應用的最外層 loop 為一個 3-stage coarse-grain 的 pipeline. 而 prefetch 行為第一個 stage.
由於並不想第一個 iteration (
k = 0) 覆蓋掉 prefetch 至 tileC 中的數值, 因此這裡選擇使用 MemFold controller. 並且建立了一個 local accum sram, 用來存放兩個來自A 與 B 的 tile 乘法的部份結果. 整個 MemFold 組成了最外部 pipeline 的第二個 stage.
這裡以使用外積的方式來計算兩個 tile 的矩陣乘法. 這裡最外層的 loop 逐步穿過內部, 直到完成這局部的矩陣. 換句話說
kk 自 tileA 選擇了一個欄位以及自 tileB 的一列. 對於 MemReduce 與 MemFold controllers 必須針對其 map 函數傳回一個 SRAM, 所以為此目的建構了 tileC_partial .
此演算中內層的 loop 逐一走過
tileA 的所有列以及 tileB 的所有欄. 這有效進行在由 kk 選出的兩向量中的外積運算(窮舉的成對乘法).MemReduce 回傳此 SRAM, 所以此特定 MemReduce 為外部 MemFold map 函數的輸出. 這也是為何有著兩個顯得奇特多餘的 {_+_} lambdas.
最後的步驟, 並且是最外層 pipeline 的第三個 stage 為將
tileC 傳輸回 DRAM 的存放動作. 下圖動畫示範如何以 triple-buffered 記憶體的方式思考 tileC.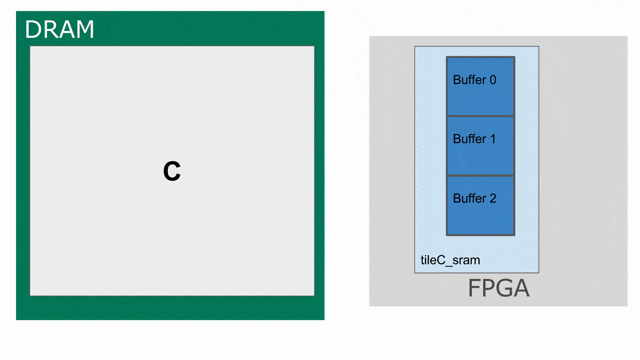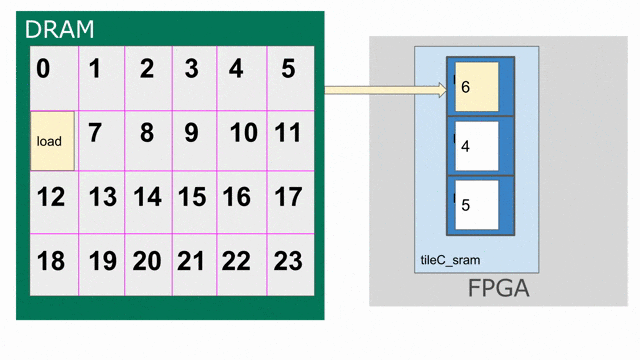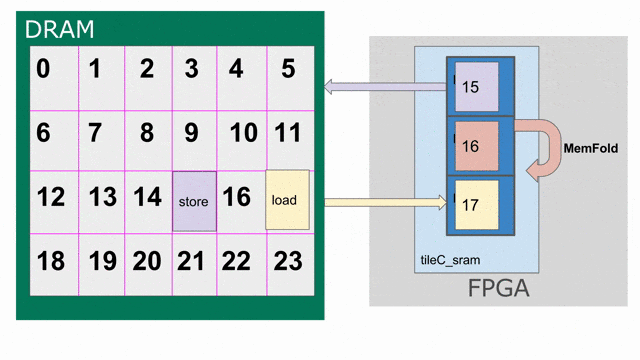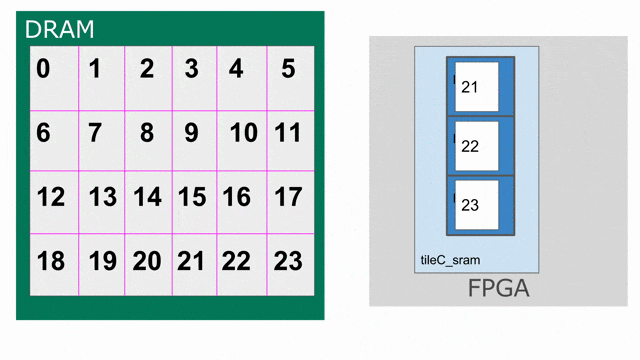
這裡使用了
getMatrix 與 printMatrix 函式來自 DRAM 取得資料並顯示這些資料結構的內容. 同樣地, 能夠使用 getTensor3, getTensor4, 與 getTensor5, 作為搭配 print 印出高維度的資料結構.Multi-dimensional Banking
import spatial.dsl._
@spatial object MatMult_outer extends SpatialApp {
type X = FixPt[TRUE,_16,_16]
def main(args: Array[String]): Unit = {
val m = args(0).to[Int]
val n = args(1).to[Int]
val p = args(2).to[Int]
val a = (0::m, 0::p){(i,j) => ((i + j * p) % 8).to[X] }
val b = (0::p, 0::n){(i,j) => ((i + j * n) % 8).to[X] }
val c_init = (0::m, 0::n){(_,_) => 0.to[X] }
val M = ArgIn[Int]
val N = ArgIn[Int]
val P = ArgIn[Int]
setArg(M,m)
setArg(N,n)
setArg(P,p)
val A = DRAM[X](M, P)
val B = DRAM[X](P, N)
val C = DRAM[X](M, N)
// *** Set mp and ip > 1
val op = 1
val mp = 2
val ip = 4
val bm = 16
val bn = 64
val bp = 64
setMem(A, a)
setMem(B, b)
setMem(C, c_init)
Accel {
Foreach(M by bm par op, N by bn par op) { (i,j) =>
val tileC = SRAM[X](bm, bn)
tileC load C(i::i+bm, j::j+bn par ip)
MemFold(tileC)(P by bp) { k =>
val tileA = SRAM[X](bm, bp)
val tileB = SRAM[X](bp, bn)
val accum = SRAM[X](bm, bn)
Parallel {
tileA load A(i::i+bm, k::k+bp)
// *** Parallelize writer by 8
tileB load B(k::k+bp, j::j+bn par 8)
}
MemReduce(accum)(bp by 1 par mp){ kk =>
val tileC_partial = SRAM[X](bm,bn)
Foreach(bm by 1, bn by 1 par ip){ (ii,jj) =>
tileC_partial(ii,jj) = tileA(ii,kk) * tileB(kk,jj)
}
tileC_partial
}{_+_}
}{_+_}
C(i::i+bm, j::j+bn par ip) store tileC
}
}
val result = getMatrix(C)
val gold = (0::m, 0::n){(i,j) =>
Array.tabulate(p){k => a(i,k) * b(k,j)}.reduce{_+_}
}
println(r"expected cksum: ${gold.map(a => a).reduce{_+_}}")
println(r"result cksum: ${result.map(a => a).reduce{_+_}}")
printMatrix(gold, "Gold: ")
printMatrix(result, "Result: ")
assert(gold == result)
}
}
這裡展示 Banking 如何在 Spatial 中作用, 以使用
tileB 作為示範記憶體. Banking 的計算方式基於 “Theory and algorithm for generalized memory partitioning in high-level synthesis” (Wang et al), 並有著次要的修改以及在 pattern 搜尋上的改進.
基本上, 對記憶體切分 bank 是藉由察看所有的存取動作並找出一個沒有衝突的 banking 方案. 更多細節請參考 關於 Spatial 論文的 Appendix A. 將 N 維度記憶體以 1D 空間方式作 bank 切分, 僅在失敗與資源利用上不必要的浪費才以多層的 bank 方式切分.
這裡設置
mp = 2 與 ip = 4. 若檢查上面使用到此平行的應用, 將發現 mp 平行化外部的 pipe 而 ip 平行化內部的 pipe. 下圖動畫顯示一個對於 tileB 在此平行化(僅考慮唯讀)下可能的 banking 方案. 請注意這並非唯一可行的方案, 其他分層與平面的方案是存在的.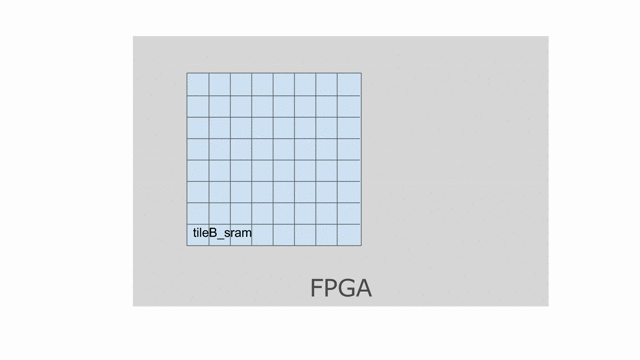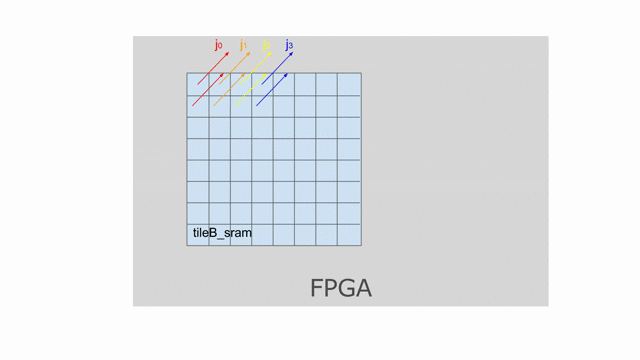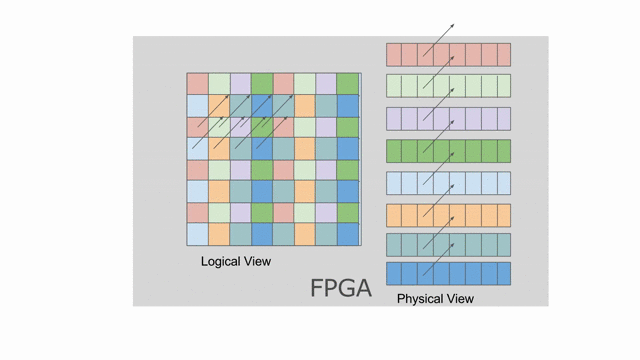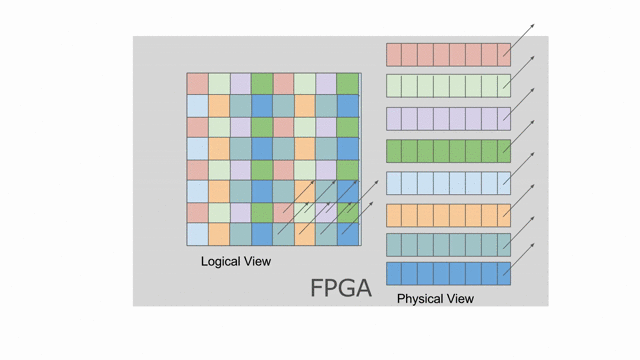
這裡選擇以 8 併行的方式平行化對
tileB 的 writer. 這表示上面的 banking 方案不再可行. 需要靜態對 SRAM 作 bank 切分來保證在記憶體存取中沒有任何 bank 衝突. 在這樣的情況中, compiler 可能會選擇如同下圖動畫顯示的平坦的 banking 方案. 請注意這動畫僅顯示以 mp = 2 與 ip = 1 所設置的 reader, 而其他不同 reader 能夠嘗試調整這些參數, 藉此來看對於記憶體會發生什麼改變.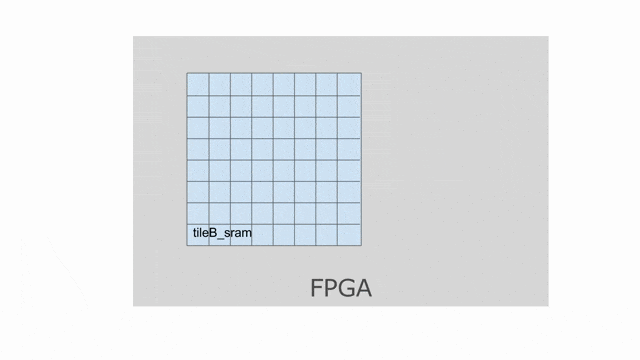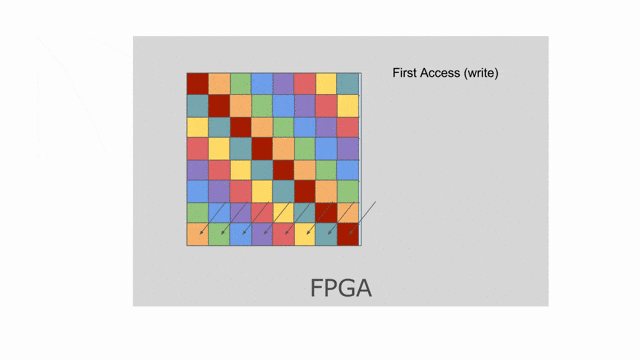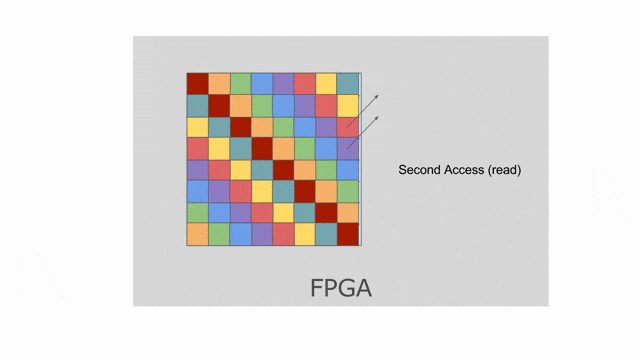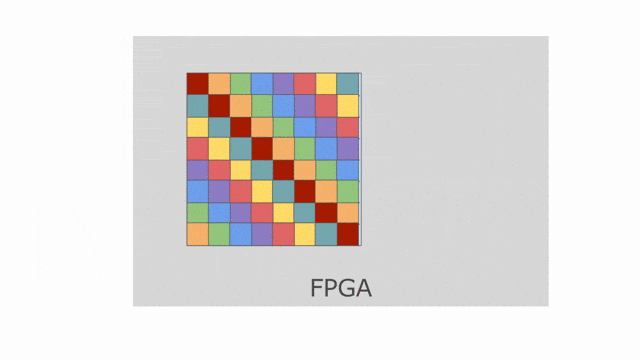


沒有留言:
張貼留言