在本節中, 將會學到下列 Spatial 的元件:
- Tiling
- Reduce and Fold
- Sequential execution and Coarse-grain pipelining
- Parallelization
- Basic buffering and banking
請注意在這裡有一些 Spatial 的應用程式.
Overview
內積 (或稱為 dot product) 是基本的線性代數 kernel, 定義為向量資料的每個單元相乘後的總和. 在此例中, 將假設資料為 signed 32-bit 定點數, 24 bits 負責整數部份, 8 bits 負責小數點以下部份. 然而相同的操作能在任何的型別上.
Basic Implementation
import spatial.dsl._
@spatial object InnerProduct extends SpatialApp {
def main(args: Array[String]): Void = {
// Define data type
type T = FixPt[TRUE,_24,_8]
// Set vector length
val len = 64
// Generate data
val vec1 = Array.tabulate[T](len){i => i.to[T]}
val vec2 = Array.tabulate[T](len)[i => (len - i).to[T]]
val d1 = DRAM[T](len)
val d2 = DRAM[T](len)
setMem(d1, vec1)
setMem(d2, vec2)
// Allocate reg for the answer
val x = ArgOut[T]
Accel {
// Create local SRAMs
val s1 = SRAM[T](len)
val s2 = SRAM[T](len)
// Transfer data
s1 load d1
s2 load d2
// Multiply and accumulate
x := Reduce(Reg[T](0))(len by 1){i =>
s1(i) * s2(i)
}{_+_}
}
// Compute "correct" answer
val gold = vec1.zip(vec2){_*_}.reduce{_+_}
// Check answer
assert(gold == getArg(x), r"Expected ${gold}, got ${getArg(x)}!")
}
}
這裡介紹最基本的向量內積實作. 下節中, 將使用這個例子來展示如何使用 Spatial API 在此應用中建立更有效率與複雜的功能. 首先簡短說明上面的程式碼.
在此實作中, 向量的長度是固定寫死的. 這尺寸用來設定 DRAMs 以及 SRAMs. 使用了
Array.tabulate以函數的索引i來建立向量的資料.
接著使用
Reduce 控制結構來定義一個 “map” 與一個 “reduce” 函數. 即為以 s1(i) * s2(i) 為 map 函數並以加法作為 reduce 函數. 對更複雜的函數, 能藉由使用 {case (a,b) => f(a,b)} 語法, 這裡 f 能表示任何使用者想要的函數. 這裡 Reduce 函數使用一個 Register 作為其第一個參數. 此例中, 使用了 Reg[T](0) 來表示它必須操作其 reduction 至一個新的型別為 T 的暫存器. 也可能直接使用 x 作為 reduction 暫存器, 這樣 reduction 即是對 ArgOut 作讀取與寫入. Reduce 接著傳回這個暫存器作為其輸出. 在這裡選擇使用一個新的 Reg 作為 reduction 暫存器並複製其值到 ArgOut 並沒有什麼特別的理由.
在 Accel 區塊之後, 撰寫了在 Host 端用以計算相同功能的程式碼, 如此來確認 FPGA 的結果是否正確. 可以檢視此代碼來了解它的作法.
若要針對特定平台編譯此應用程式, 請參考 Targets 頁面
Tiling, Reduce, and Fold
import spatial.dsl._
@spatial object InnerProduct extends SpatialApp {
def main(args: Array[String]): Void = {
type T = FixPt[TRUE,_24,_8]
// *** Set tile size as compile-time constant
val tileSize = 64
// *** Allow dynamically sized array
val len = ArgIn[Int]
setArg(len,args(0).to[Int])
// *** Use ArgIn to generate data and configure DRAM
val vec1 = Array.tabulate[T](len){i => i.to[T]}
val vec2 = Array.tabulate[T](len)[i => (len - i).to[T]]ArgIn
val d1 = DRAM[T](len)
val d2 = DRAM[T](len)
setMem(d1, vec1)
setMem(d2, vec2)
val x = ArgOut[T]
Accel {
// *** Create local SRAMs with fixed tile size
val s1 = SRAM[T](tileSize)
val s2 = SRAM[T](tileSize)
// *** Loop over each tile
x := Reduce(Reg[T](0))(len by tileSize){tile =>
s1 load d1(tile::tile+tileSize)
s2 load d2(tile::tile+tileSize)
// *** Return local accumulator to map function of outer Reduce
Reduce(Reg[T])(0))(tileSize by 1){i =>
s1(i) * s2(i)
}{_+_}
}{_+_}
}
val gold = vec1.zip(vec2){_*_}.reduce{_+_}
assert(gold == getArg(x), r"Expected ${gold}, got ${getArg(x)}!")
}
}
在多數的應用程式中, 有著一些在編譯時期未知的演算屬性. 資料結構可能是動態配置大小且 FPGA 的 synthesize 可能耗時數小時, 因此會希望儘可能保有演算法的彈性.
第一個帶入彈性的方法是藉由 “tiling”. 這表示允許在 Host 端使用動態資料結構, 而保持在 Accel 中保持固定屬性. 上面重新撰寫的程式展示了支援 tiling 所需要的更動. 接著來討論這些修改.
首先必須在編譯時期固定一個 tile size. 在本例中, 設定為 64. 請參考 DSE (Design Space Exploration)中的教學來學習如何如此般自動調整參數. 接著必須以
ArgIn 將向量大小傳給 FPGA. 在此透過第一行指令參數來設定.
當建立資料結構, 能夠交替使用
ArgIn 或是指令行的 args(0). 請注意若選擇使用 ArgIn 必須在使用前設定. 這是因為這部份程式是依序在 CPU 端運作. 在複寫之前預設的 ArgIn 數值為 0.
在 Accel 中, 必須增加另一個迴圈來走過所有的 tiles. 在一個 tile 中, 必須執行在先前所展示的相同程式碼. 在 outer
Reduce, 以步距為 tile size 的方式走過完整的長度. 而在 local memory 中, 一次僅讀取一個 tile.
一開始有件稍微棘手的事, inner
Reduce 將傳回的純量放在一個暫存器中. 而這個在暫存器的純量數值被 outer Reduce 使用作為其 map function 的結果.
另外也有可能向量的長度無法被 tile size 所整除. 此時必須處理邊界的情況. 在這程式中有著兩個方式來處理. 首先, 能夠加一行程式碼到 outer
Reduce:val actualTileSize = min(tileSize, len - tile)
接著使用這來取代
tileSize, 由於這在最後一次 iteration 中能夠選擇有多少剩下的單位.
有一些與硬體複雜度相關的 tile 傳輸, 其大小與邊界並非靜態已知. 另一個有效的選項為遮蔽掉在 inner
Reduce的 map 函數數值. 精確地說, 能夠將函數改為:mux(i + tile <= len, s1(i) * s2(i), 0.to[T])
這方式, 當手上單位的 global index 落在原始向量的範圍時, 會傳回兩個單位的乘積. 其他的部份將會以型別 T 來回傳數值 0.
最後在此範例介紹
Fold 的概念. Fold 類似於 Reduce, 除了它在迴圈的第一次 iteration 並不使用累加暫存器的初始值. 在打算累加數值到已存在於暫存器中的數值的情況下, 能夠使用 Fold. 能藉由改變外部迴圈為 Fold(x)(…){…}{…} 而不改變結果, 由於 Fold 僅執行一次, 而由於是個未初始化參數 x 自 0 開始. 這並非一個與義上有用的範例, 但這是另一個簡單的方式來撰寫這個應用程式.Coarse-Grain Pipelining
import spatial.dsl._
@spatial object InnerProduct extends SpatialApp {
def main(args: Array[String]): Void = {
type T = FixPt[TRUE,_24,_8]
val tileSize = 64
val len = ArgIn[Int]
setArg(len,args(0).to[Int])
val vec1 = Array.tabulate[T](len){i => i.to[T]}
val vec2 = Array.tabulate[T](len)[i => (len - i).to[T]]
val d1 = DRAM[T](len)
val d2 = DRAM[T](len)
setMem(d1, vec1)
setMem(d2, vec2)
val x = ArgOut[T]
Accel {
val s1 = SRAM[T](tileSize)
val s2 = SRAM[T](tileSize)
// *** Enfore pipelined execution
x := Pipe.Reduce(Reg[T](0))(len by tileSize){tile =>
s1 load d1(tile::tile+tileSize)
s2 load d2(tile::tile+tileSize)
// *** Enforce pipelined execution
Pipe.Reduce(Reg[T])(0))(tileSize by 1){i =>
s1(i) * s2(i)
}{_+_}
}{_+_}
}
val gold = vec1.zip(vec2){_*_}.reduce{_+_}
assert(gold == getArg(x), r"Expected ${gold}, got ${getArg(x)}!")
}
}
在本節重新撰寫此應用, 會發現兩項改變. 即以
Pipe 標籤註明兩個 Reduce 迴圈. 這讓它們以 pipelined 的方式運作, 而 compiler 並不允許複寫這個行為. 若沒有任何標明, compiler 預設使用 Pipe 但若 DSE 發現一個更有效的設計則可能會使用不同的標籤. 現在討論 controller 如被排程, 以及這在 inner controller 與 outer controller 所代表的意義.
在 Spatial 中, 一個 controller 不是個 inner 就是個 outer controller. 可以複習一下 Control Flow 教學,
- Inner controllers 僅包含指令 (i.e.- arithmetic, memory access, muxing, etc.)
- Outer controllers 包含最少一個其他的 controller (i.e.-
Foreach,Reduce,FSM, etc.) 以及不消耗 FPGA 資源的 “短暫” 操作 (i.e.- bit slicing, struct concatenation, etc.)
在上面程式碼的例子, outer
Reduce 包含兩個 loads (在 compiler 中會以特定的 controller sub-tree 取代來處理到 DRAM 的 transaction) 以及其他 Reduce controller. 由於僅包含一個為數學指令的乘法運算, 這個 Reduce 為一個 inner controller.
對此兩個 controller 增加了
Pipe 標示, 這表示期望 compiler 儘可能地對這些 controller 作 pipeline 平行化. 在 outer controller 中, 這代表這些 stage 會以這方式執行:
兩個
loads 將平行地執行 tile = 0 (由於並沒有資料相依性). 當兩者都完成時, Reduce 相會以 tile = 0 來執行, 而 loads 將以 tile = 64 執行, 以此類推. 以軟體的術語, 這特定的 coarse-grain pipelining 的例子為 “prefetching,” 但是這概念能被廣泛地應用在 Spatial 中來以任意深度的 pipeline 來重疊任何的運算.
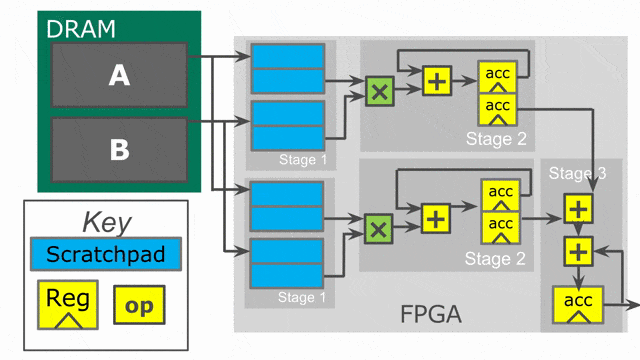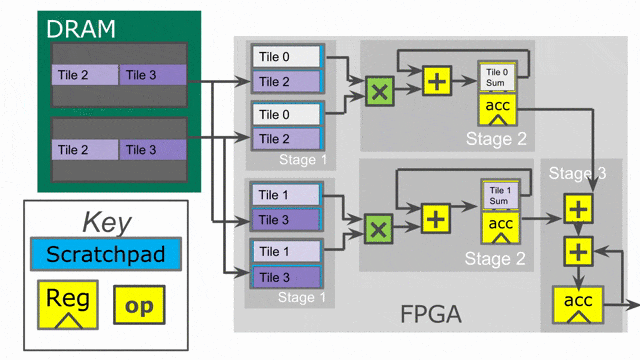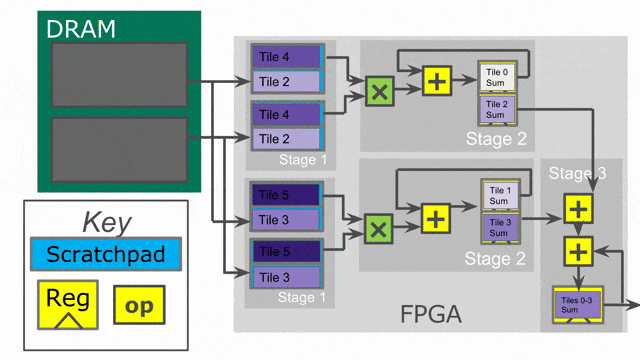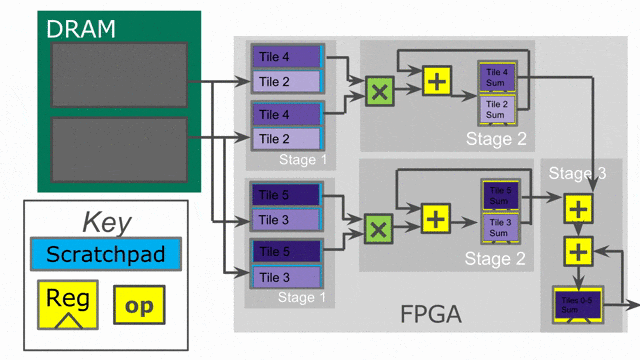
Outer controller 的 Pipelining 需要 compiler 插入 N-buffered 記憶體. 在這個特定的例子中, 兩個 SRAMs 都將會是 double buffered, 如此在 controller 的第一個 stage 中資料載入到 SRAM 不會覆蓋到 controller 的第二個 stage 所正在自 SRAM 讀取出的資料.
對於 inner controller, 這表示硬體將在每個 cycle 發出新的
i 值. 儘管這乘法運算可能有著 6 cycles 的延遲, 一旦 pipeline 以 steady-state 狀態運作, 能夠預期在 6 cycles 中得到 6 個新結果. 在更為複雜的例子中, 甚至可能對整個主體或是部份有著 loop-carry 相依性, 這時 compiler 會選擇 controller 的 initiation interval來保證正確性.
除了
Pipe, Spatial 支援 Sequenced 與 Stream 的標示.Sequenced 表示在 outer controllers 中完全沒有任何 pipelining, 以及 initiation interval 等同於所有主體中 inner controllers 的延遲. 使用這個標示, counter 在增加之前, 會將單一數值的傳播給每一個 stage. 雖然較 Pipe 為緩慢, 其消耗較少的資源, 且能作為解決 loop-carry 相依性問題的方案.Stream 代表一個 control schedule 在資料層級作 pipelined. 一個 two-stage pipeline 的 Stream controller 表示任何在這 pipeline 的 stage, 一旦輸入的 steam 型態的記憶體 (FIFOs, DRAM Buses, etc.) 有可取的資料且其輸出的stream-style 記憶體準備好接收資料就會運行. 將在後續的教學中有更詳細的討論.
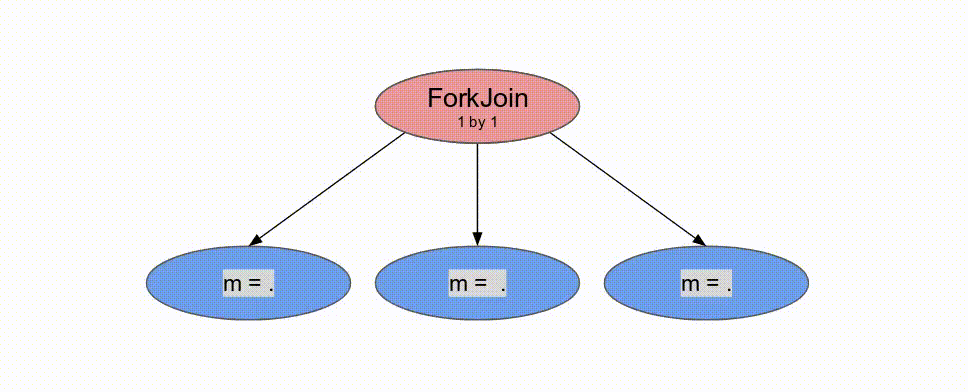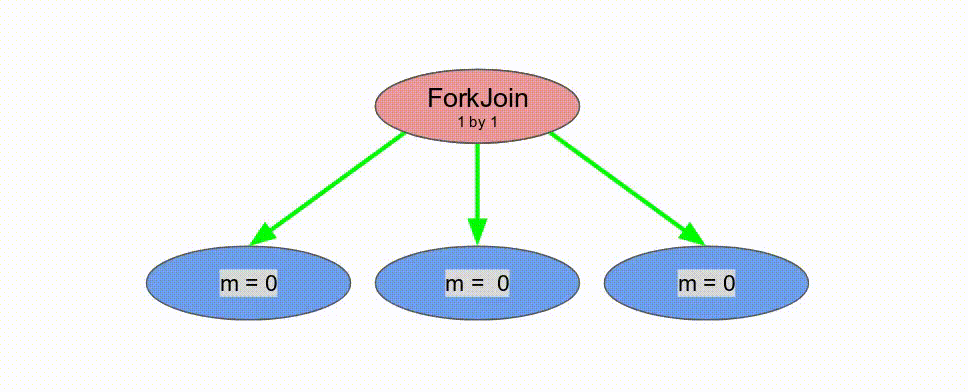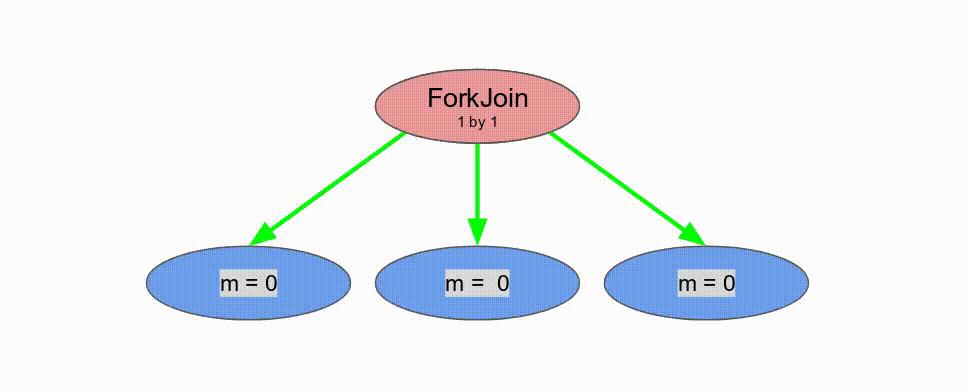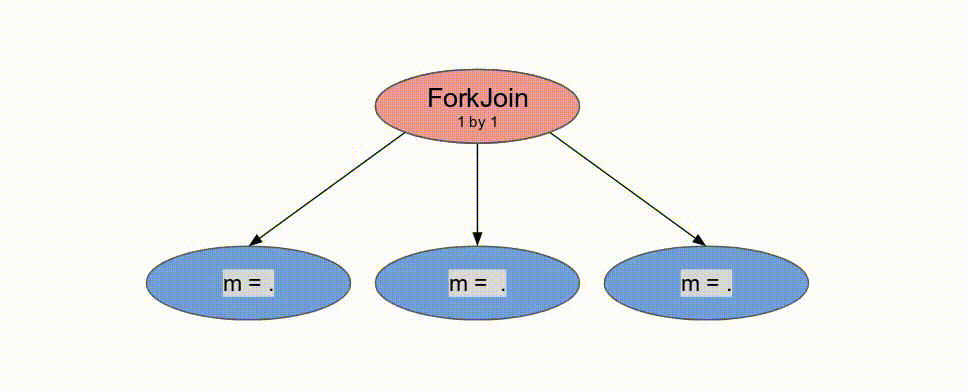
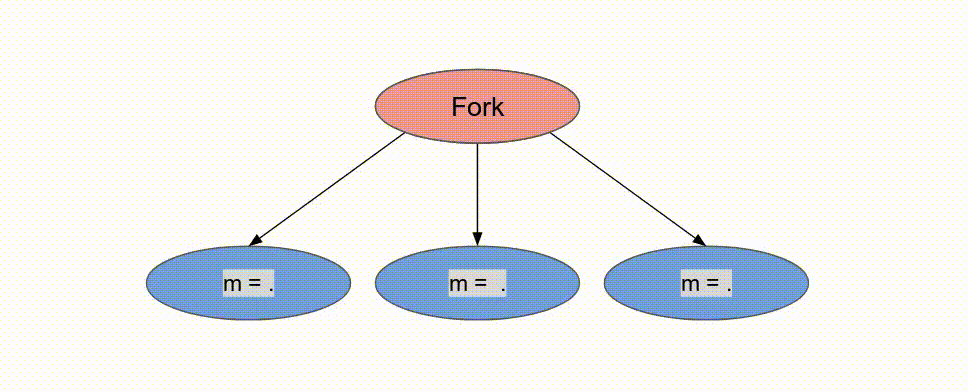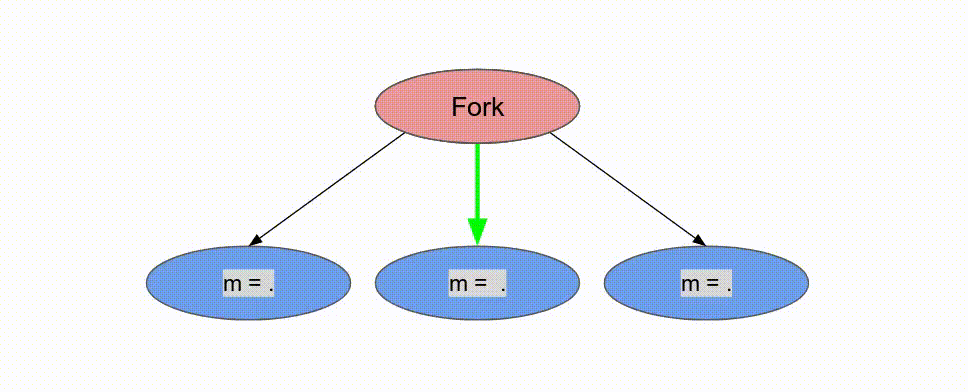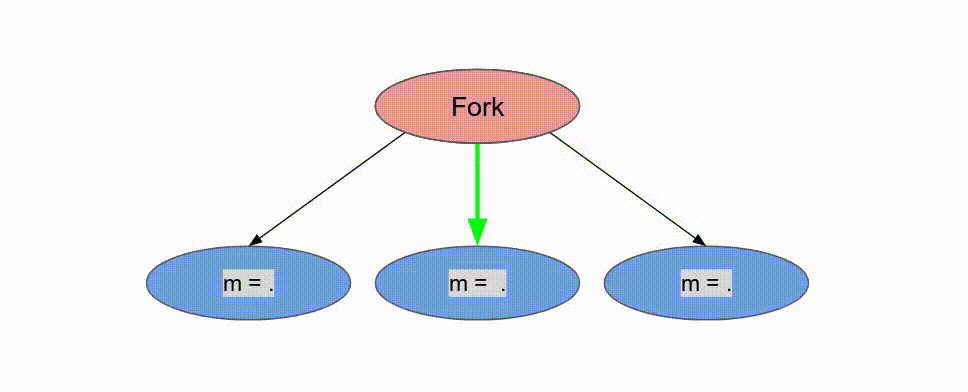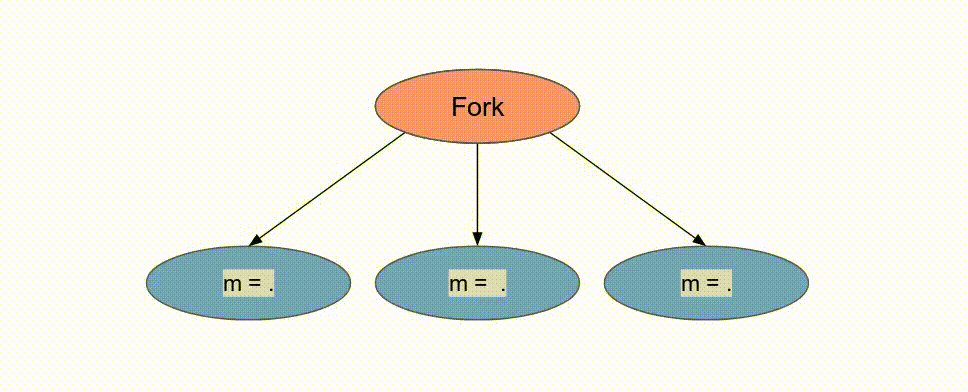
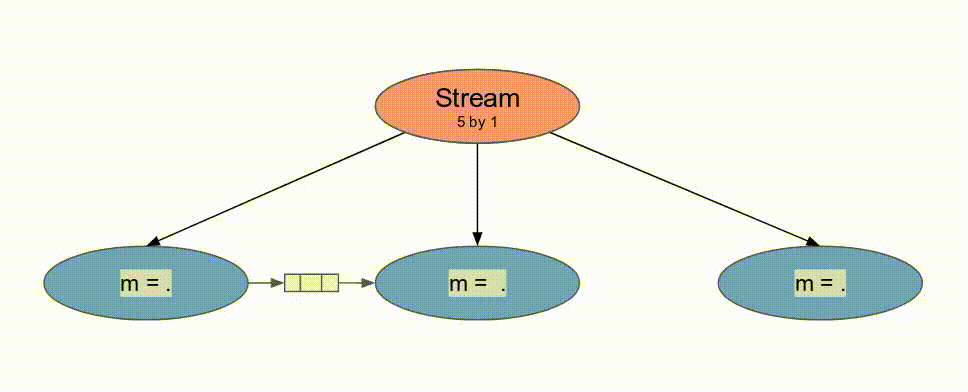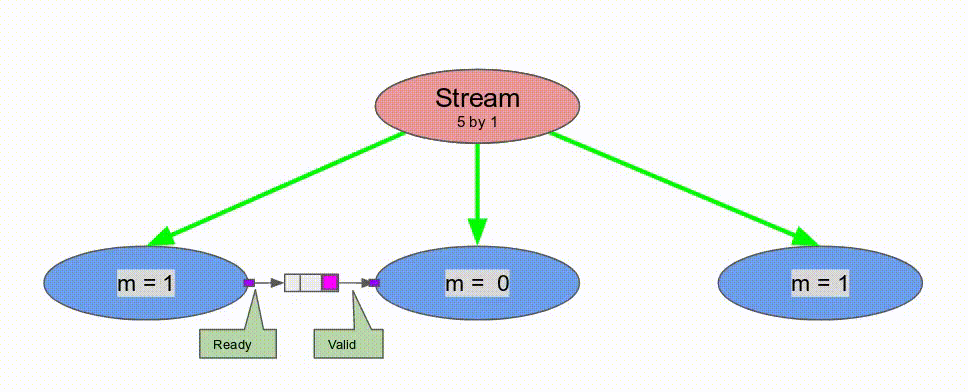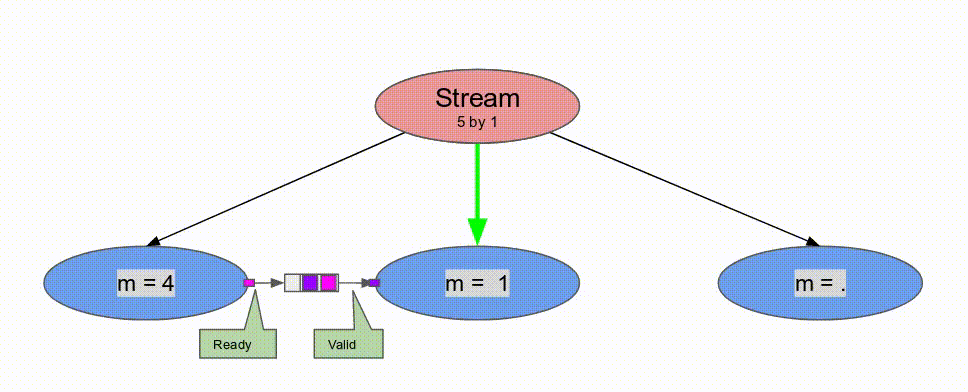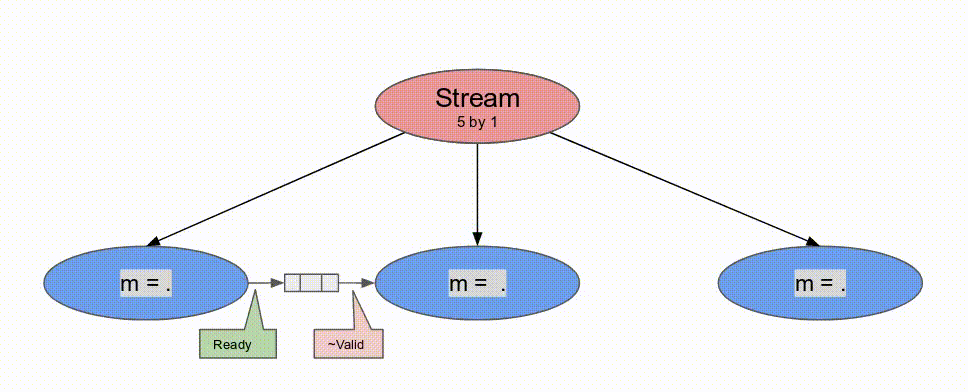
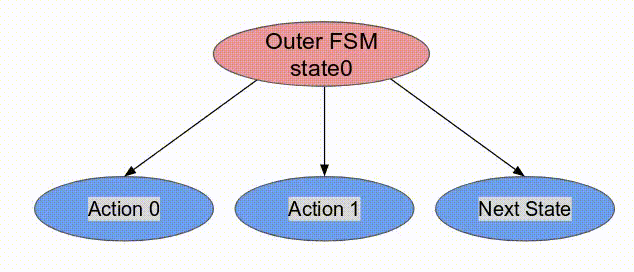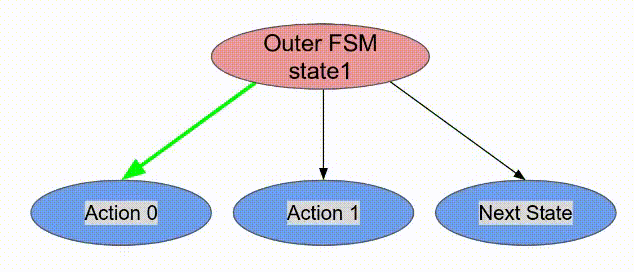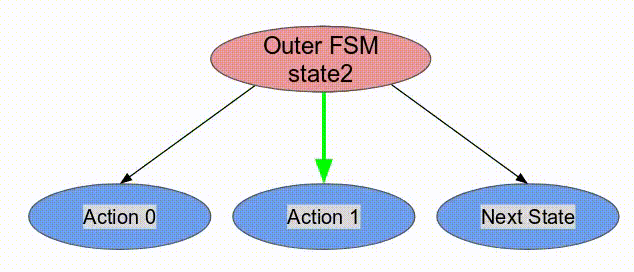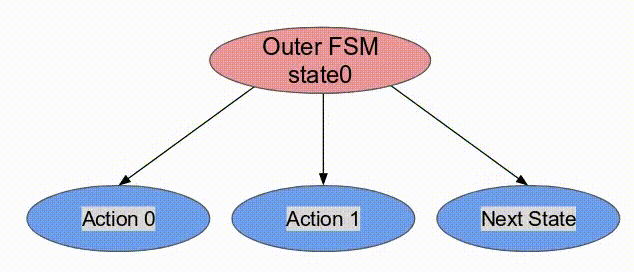
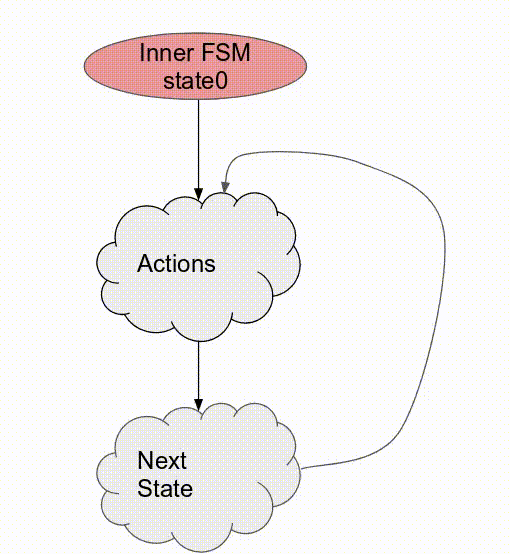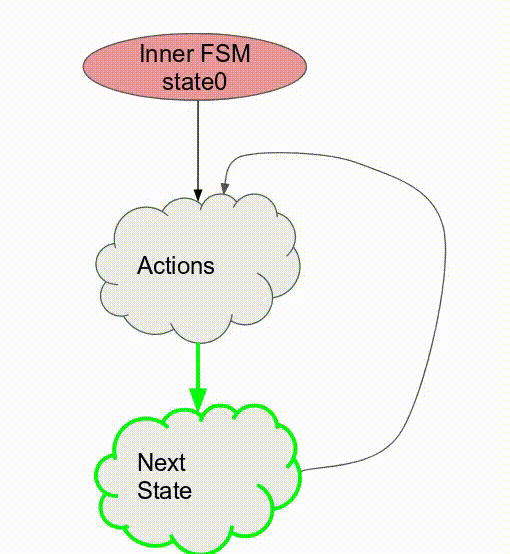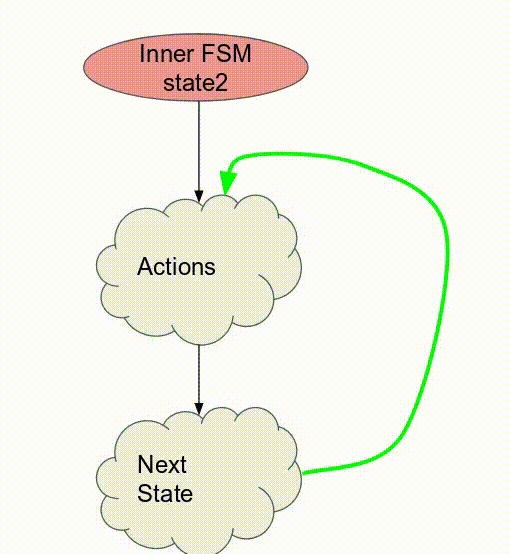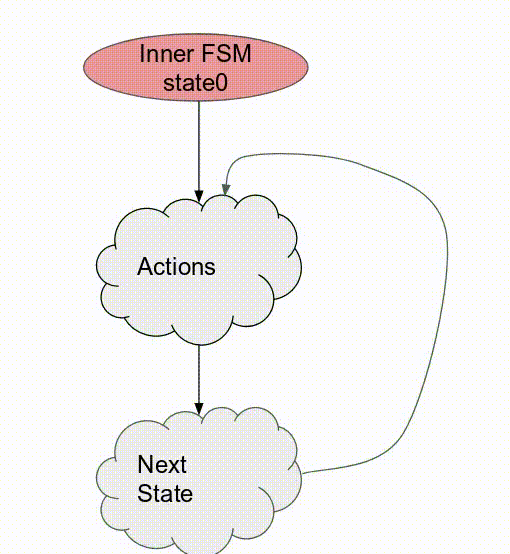
下面的動畫演示了以
Pipe 與 Sequenced 標示來執行這個程式的過程.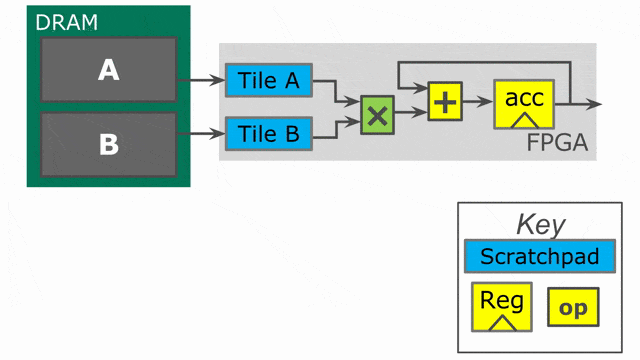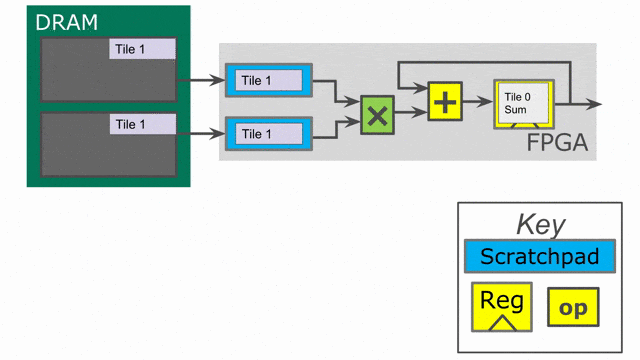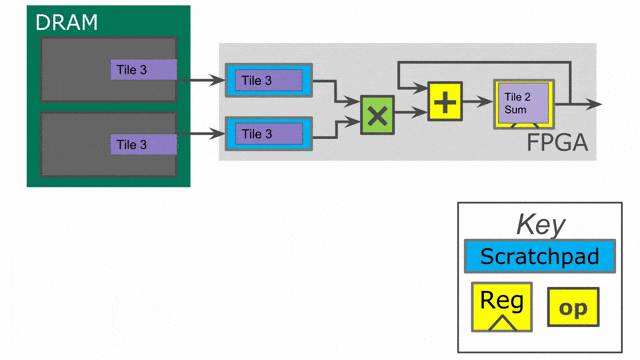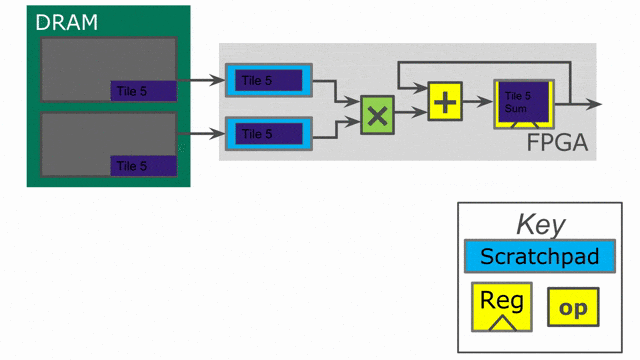
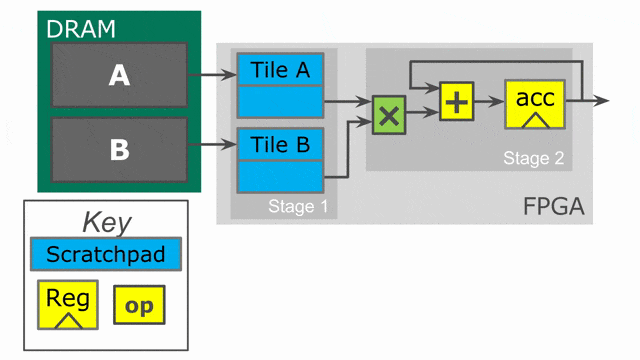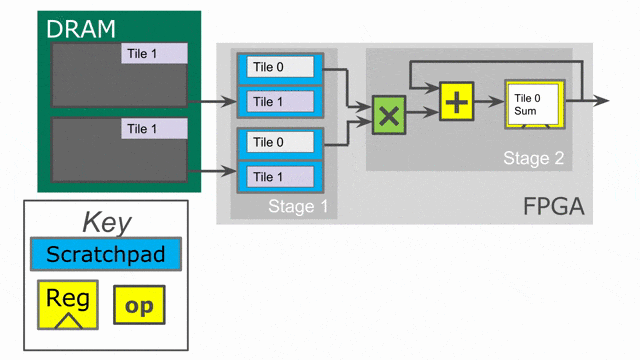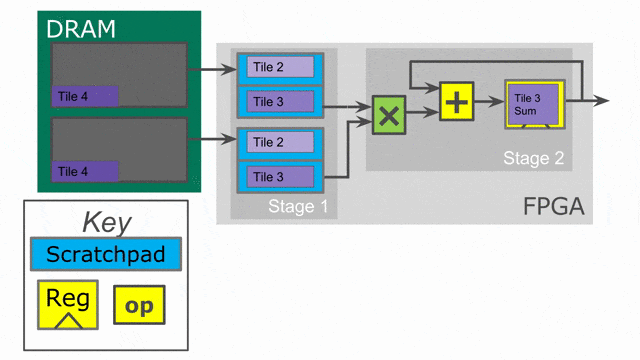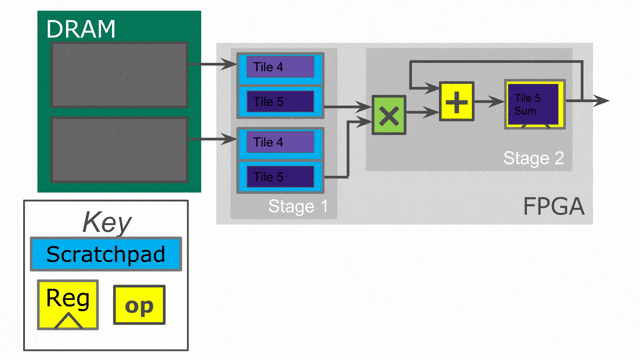
Parallelization
import spatial.dsl._
@spatial object InnerProduct extends SpatialApp {
def main(args: Array[String]): Void = {
type T = FixPt[TRUE,_24,_8]
val tileSize = 64
val len = ArgIn[Int]
setArg(len,args(0).to[Int])
val vec1 = Array.tabulate[T](len){i => i.to[T]}
val vec2 = Array.tabulate[T](len)[i => (len - i).to[T]]
val d1 = DRAM[T](len)
val d2 = DRAM[T](len)
setMem(d1, vec1)
setMem(d2, vec2)
val x = ArgOut[T]
Accel {
// *** Parallelize tile
x := Reduce(Reg[T](0))(len by tileSize par 2){tile =>
// *** Declare SRAMs inside loop
val s1 = SRAM[T](tileSize)
val s2 = SRAM[T](tileSize)
s1 load d1(tile::tile+tileSize)
s2 load d2(tile::tile+tileSize)
// *** Parallelize i
Reduce(Reg[T])(0))(tileSize by 1 par 4){i =>
s1(i) * s2(i)
}{_+_}
}{_+_}
}
val gold = vec1.zip(vec2){_*_}.reduce{_+_}
assert(gold == getArg(x), r"Expected ${gold}, got ${getArg(x)}!")
}
}
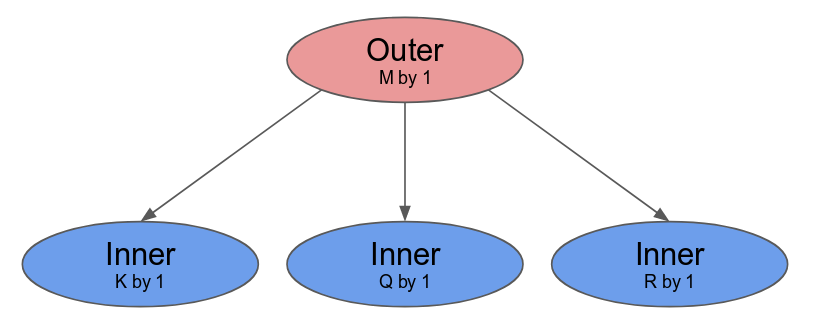
在此例中, 將加入兩個平行化標示. 以(平行化因子為) 2 的方式平行化 outer loop, 且以(平行化因子為) 4 的方式平行化 inner loop. 當在 Spatial 之中使用平行化, 必須思考相關的 iterator (在此例中的
tile 與 i) 被平行化參數所向量化. 這個 iterator 並不會一次顯示一個數值, 而將會一次顯示多個連續數值. 這表示外部迴圈的第一個 iteration, 將平行地處理 tile = 0 與 tile = 64.
Compiler 將會以一次 2 個的方式展開(unroll)外部迴圈, 這表示將會複製整個在其中的控制結構來提供平行運作的硬體. 請注意必須將 SRAM 的宣告搬至迴圈內部, 如此 compiler 才會一併展開存在其中的記憶體宣告. 對於此 controller 的兩條 lane 都需要專屬的 SRAMs, 因此需要展開 SRAMs 來搭配所有的一切.
而 inner loop 有著 4 的平行因子, 這表示一次將發出 4 個單元到 map 函數中.(i.e.-
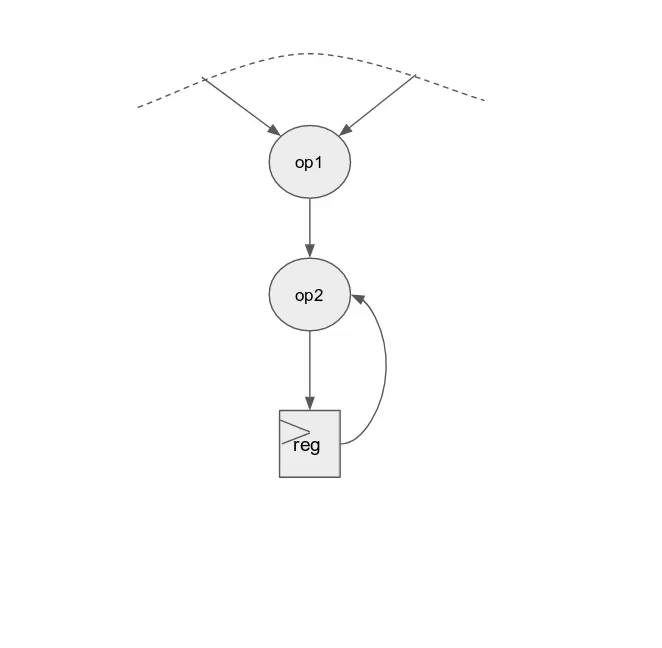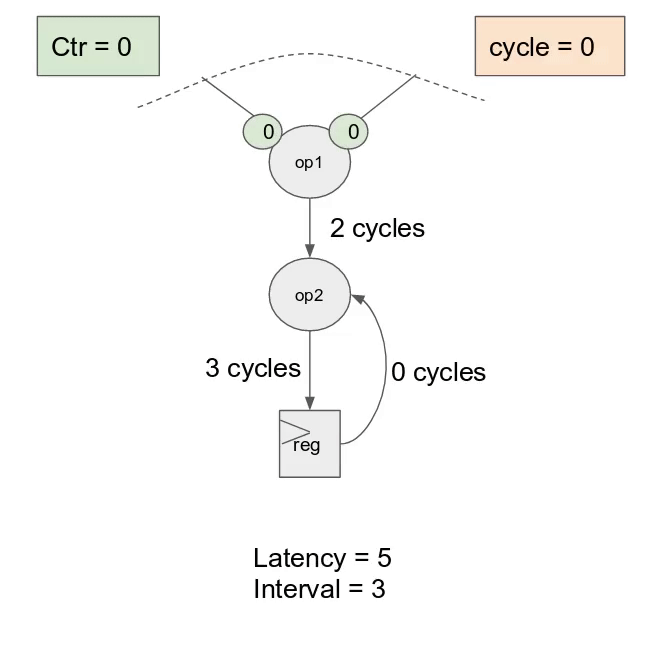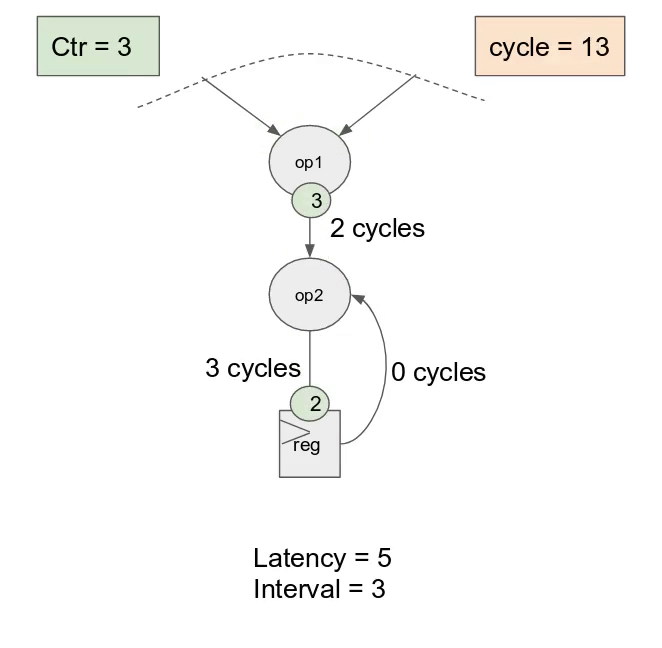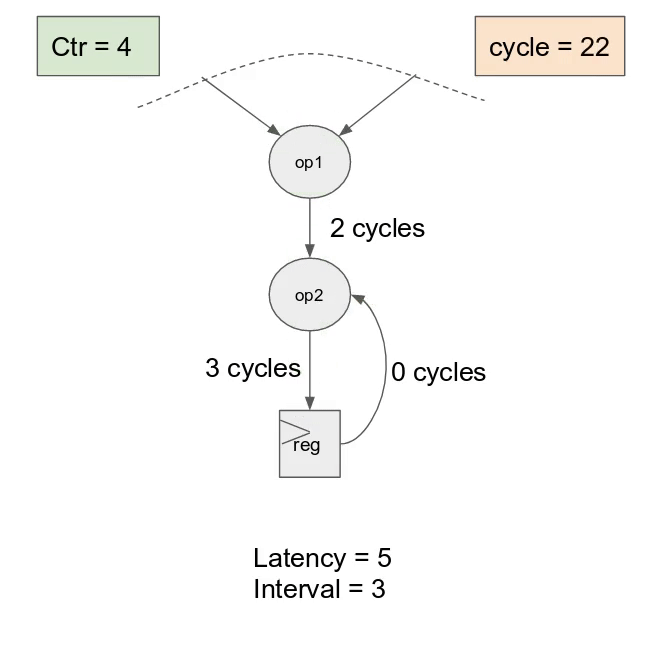
i = 0, i = 1, i = 2, and i = 3), 以及一個有著深度為 log2(4) = 2 的總和樹將產生來以最小延遲累加來自所有 lane 的數值.
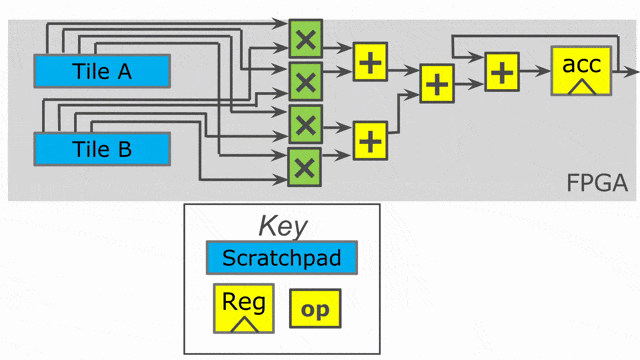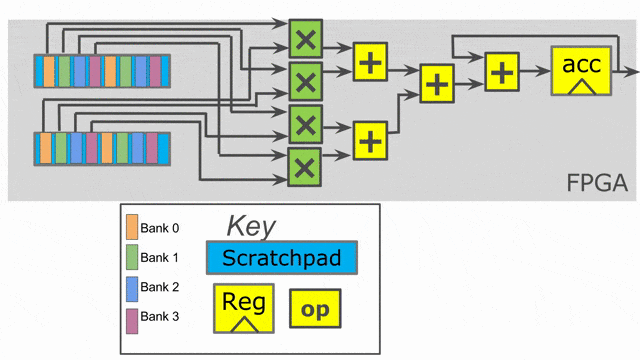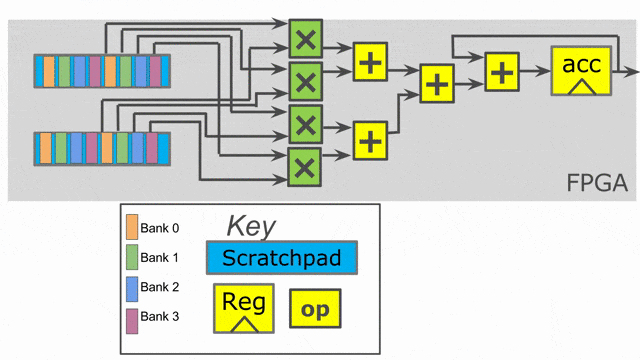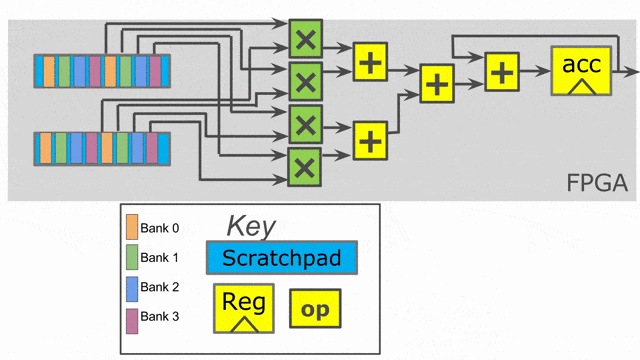
下圖動畫顯示了此應用以 outer parallelization 與 inner parallelization (個別地) 所生成的硬體.